Researchers win a 'impossible' game by using 'quantum telepathy'

A new, fun demonstration of quantum pseudotelepathy could lead to improvements in communication and computing.

Bridge is a card game that is played by two teams of two. In order to win, one player must let their teammate know how strong their hand is. It would help to be able to talk to each other. But telepathy doesn't exist, right?

Yes, that's right. But for decades, physicists have thought that if bridge were played with quantum mechanics-based cards, it should be possible to do something that looks a lot like telepathy. Now, scientists in China have tested this so-called quantum pseudotelepathy, but not in quantum bridge, but in a two-player quantum competition called the Mermin-Peres magic square (MPMS) game. To win, the players have to coordinate their actions without telling each other what they are doing. When used wisely, quantum pseudotelepathy lets the players win every round of the game, something that would not be possible without it. The experiment, which is done with laser photons, tests the limits of what quantum mechanics lets particles do when it comes to sharing information.

Arul Lakshminarayan of the Indian Institute of Technology Madras, who was not involved in the experiment, says that the work is "a beautiful and simple direct implementation of the Mermin-Peres magic square game." He also says that part of its beauty comes from how elegantly it proves that a quantum system's state is not well known before it is measured, which is often thought to be the most confusing thing about quantum mechanics. He says, "These quantum games seriously challenge our common idea that things have pre-existing properties that can be seen by observing them."

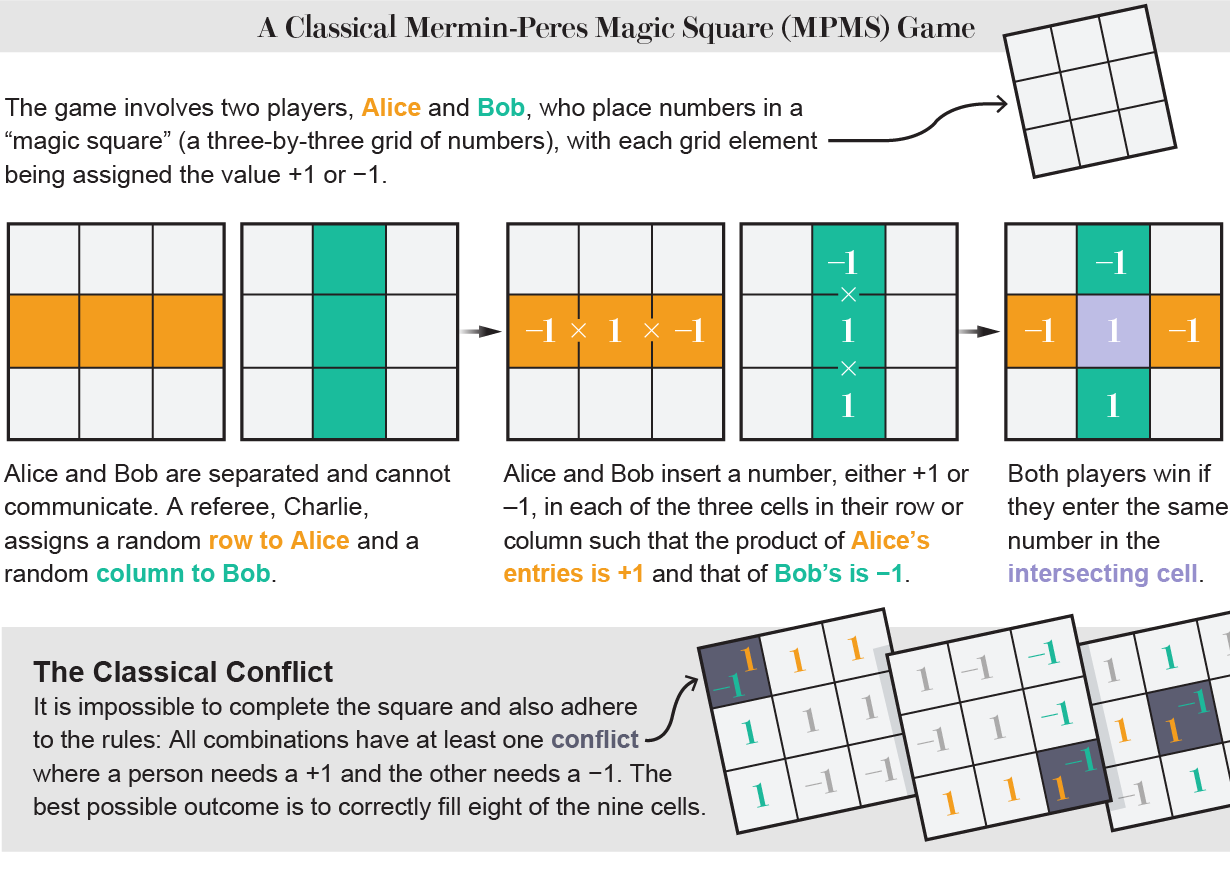
Asher Peres and David Mermin, both quantum physicists, came up with the MPMS in 1990. It's played by two people named Alice and Bob, as is usual in quantum-mechanical thought experiments. They have to fill in a "magic square," which is a three-by-three grid of numbers, where each number has a value of either +1 or -1. In each round, the referee, Charlie, gives a row to Alice and then a column to Bob at random (there are nine such row-and-column combinations). The players have to tell Charlie what values of +1 or -1 to put in their three grid spaces. As with any magic-square puzzle, like Sudoku, the sums of each row and column must meet certain rules. In this case, the product of all the entries in a row must be +1, and the product of all the entries in a column must be -1. Alice and Bob win a round if they both give the same value to the grid element where the column and row overlap.

Classically, you can't win all rounds because, even if Alice and Bob are right every time, there will always be one round for every filled square where their guesses will be wrong. The most they can do is win eight of every nine games.

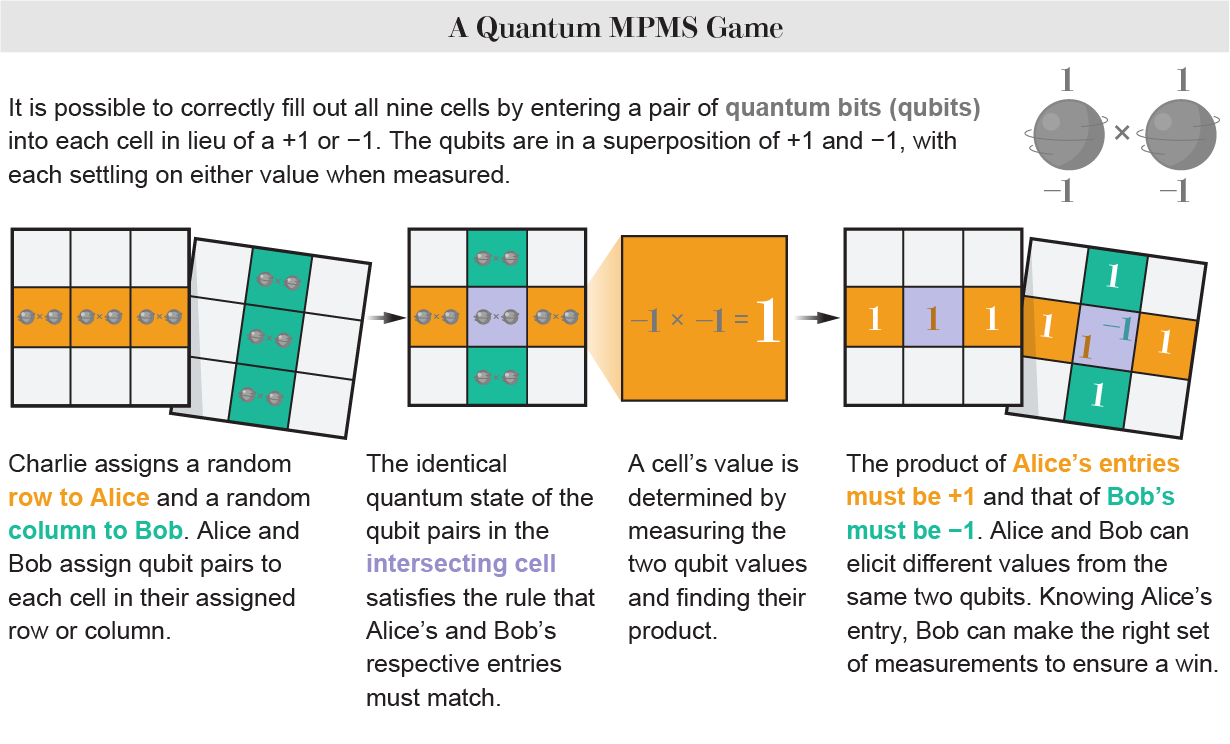
But let's say that Alice and Bob can use this quantum strategy: Instead of giving each grid element a value of +1 or -1, they give it a pair of quantum bits (qubits), which can be measured as either +1 or -1. The value that each player gives to a certain grid element is found by adding up the values of the two qubits and multiplying them together. Now, the classical conflict can be avoided because Alice and Bob can get different values from the same two qubits depending on how they measure them. There is a certain way to measure that will make sure that the winning criteria for any given round, which is that the sums of Alice's and Bob's three entries are +1 and -1, respectively, are met for all nine different ways the rows and columns can be arranged.

There is a catch to this plan, though. Alice and Bob need to work together to figure out which of their three grid pieces overlaps with the other player's so they can make the right set of measurements. But this doesn't matter in the MPMS because they measure the same three qubit pairs one after the other. This means that the pair that gets to Bob already has a record of how Alice measured those quibits. This means that they can share information with each other.

In 1993, Mermin showed that the MPMS could be used to show something called contextuality, which has to do with quantum physics. Contextuality is the idea that the result of a quantum measurement may depend on how the measurement is done. This idea was first put forward by the Northern Irish physicist John Stewart Bell in 1966. Classical measurements of a system will always give the same results, no matter what order they are done in. But this isn't always true for quantum measurements. In the MPMS, the contextuality comes from the fact that the measurement for a given qubit pair may give a different result depending on which other two pairs are also being measured.

But what if we stopped everyone in the MPMS from talking to each other by giving Alice and Bob different qubit pairs and telling them they couldn't talk about how to measure them? Then each player can only win nine times out of nine if they correctly guess what the other player will do. But in a study published in 2005, quantum theorist Gilles Brassard of the University of Montreal and his colleagues showed that the players can use quantum principles to win every round without talking to each other. They called this "quantum pseudotelepathy."

In this strategy, each of the two pairs of qubits sent to Alice or Bob is mixed up with a qubit used by the other player. The properties of entangled particles are linked, so if Alice measures the value of her particle, this changes the value of Bob's particle as well. If Alice's qubit is found to be +1, then Bob's must be -1. Before it is measured, there is no way to know if Alice's qubit is +1 or -1, but Bob's will always be the opposite. Importantly, a property that is shared by two particles is called "nonlocal." This means that it is not "local" to either particle, but is shared by both. Even if the particles are very far apart, the pair must still be thought of as a single, nonlocal object. Quantum theorist Adán Cabello of the University of Seville in Spain came up with the same basic idea for winning a quantum game in 2001. He called it "all or nothing," and it was later shown to be the same as the nonlocal (pseudotelepathic) MPMS.

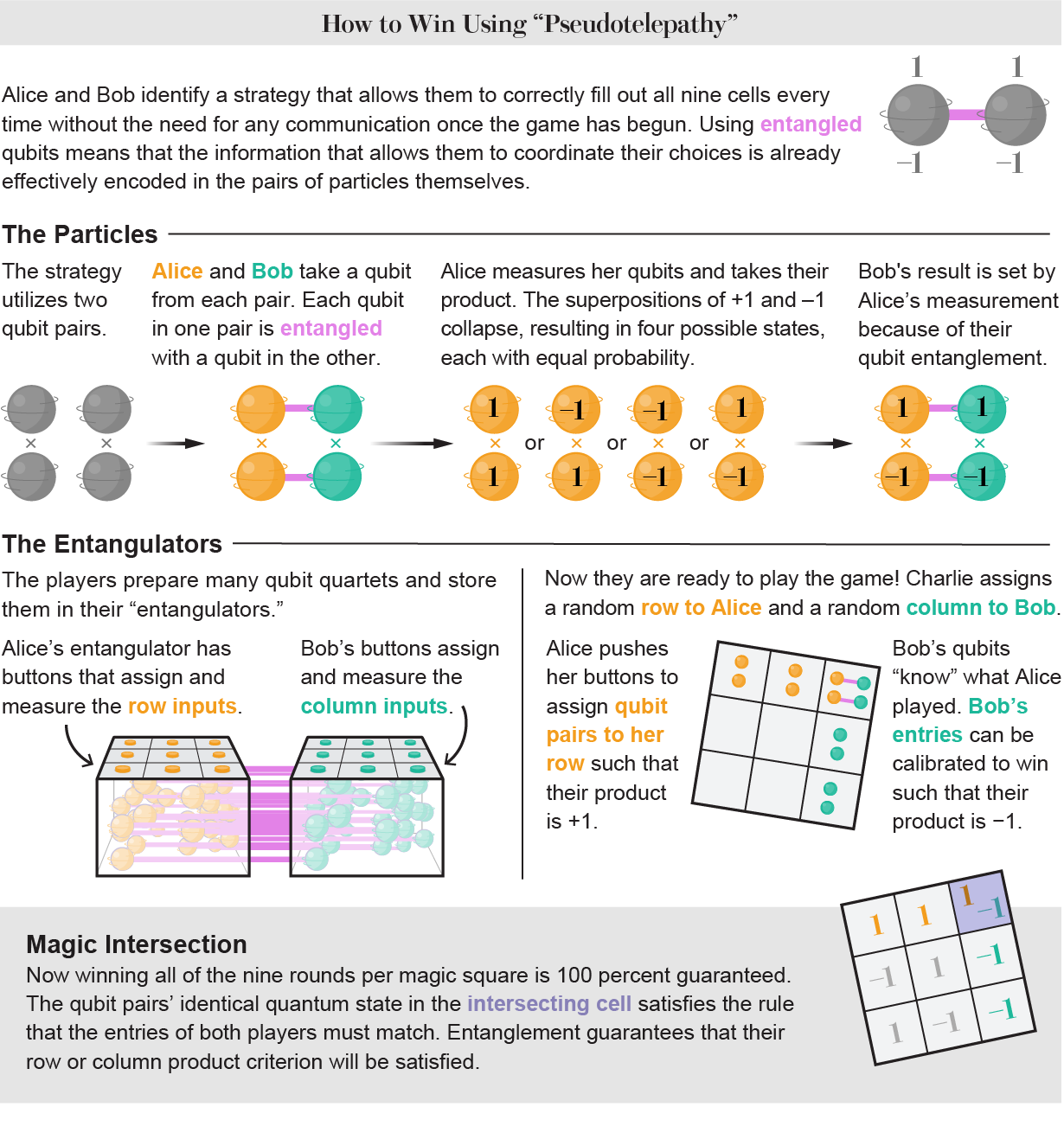
Some scientists think that the most basic part of quantum mechanics is entanglement. It means that particles share information in some way. This is the key to using entanglement for quantum pseudotelepathy: Alice and Bob don't have to talk to each other to coordinate their actions, because the information they need is already shared between the particles in each pair.

Both contextuality and nonlocality can be thought of as "quantum resources" that can be used to get an edge over traditional ways of processing information. In quantum computing, for example, entanglement between the quantum bits is often the tool that helps find a solution to a problem faster than a classical computer could.

Physicists have used entangled photons to show over and over again that Cabello's all-or-nothing game works in the real world. But while those experiments showed how entanglement could give a "quantum advantage" by beating classical performance, Kai Chen of the University of Science and Technology of China, Xi-Lin Wang of Nanjing University in China, and their colleagues have come up with a new experiment that they say uses the full protocol to guarantee a win every time—real, consistent quantum pseudotelepathy.

In an ideal situation, Alice and Bob would set up a lot of sets of four qubits before the game starts. Each set of four would have two pairs of qubits that are linked together. One of each pair would go to Alice, and the other would go to Bob. The researchers say it is very hard to make two pairs of photons that are linked together for each round of the game. For one thing, their machine has a low chance of making even a single pair of entangled particles, so making two at once would be very unlikely. And this optical implementation can't really find two pairs at the same time, which is what the pseudotelepathic MPMS needs.

Instead, Chen, Wang, and their coworkers made single-photon pairs and mixed up their polarization state and something called their orbital angular momentum. The photons were in ultrashort laser pulses that lasted only 150 femtoseconds, and they were mixed up by sending them through two so-called "nonlinear optical crystals." First, a thin slice of barium borate split a single photon into two lower-energy photons with similar angles of rotation. Then, by sending them through a crystal of a yttrium-vanadium compound, they were also mixed up in terms of their polarization.

To show that they were almost always right, the researchers had to improve their ability to find the entangled photons so that almost none of them could get away without being seen. Even so, the experiment can't reach the theoretical limit exactly, but the researchers were able to show that they could win every round with a 91.5–97% chance. This means that you can reliably beat the classic eight-out-of-nine limit after playing a total of 1,009,610 rounds out of 1,075,930.

Chen says that the pseudotelepathic MPMS game takes advantage of the strongest connection between particles that quantum mechanics can offer. He says, "Our experiment looks into how to make extreme quantum correlations between particles." If these correlations were any stronger, they would mean that information could be sent faster than light, which many other experiments have shown is not possible.

Mermin says that even though the experiment was successful, this doesn't show anything new about quantum mechanics other than that it works the way we thought it would. Cabello doesn't agree with everything. He says that the work is more than just an experimental tour de force; it also shows a new way that quantum rules can be used by using two sources of quantum advantage at the same time. One source is related to nonlocality, and the other is related to context. Cabello says that physicists should be able to learn more about how the two effects are related if they look at them both at the same time.

Also, each of these resources could be used in different ways in quantum processing, which makes it more flexible. "For example, nonlocality can be used for secret communication [using quantum cryptography], and contextuality can be used for quantum computing," says Cabello. In this situation, Bob could, for example, set up secure communication with Alice and do a computation with Charlie faster than is possible with traditional methods.

Lakshminarayan says that when shared entanglement is used in these experiments, it "leads to effects that seem like magic." But since quantum mechanics is often used as a fake reason for pseudoscientific claims, isn't calling the phenomenon "pseudotelepathy" asking for trouble? Mermin says, "It's a bad word that can be interpreted in crazy ways." But Cabello agrees, and he also knows that names that sound interesting can help spread the word about a trend. "Don't fool yourself," he says. "You and I are probably talking to each other because of the word "pseudotelepathy."

========

Follow us on Google News