More On: Pi day
Fun facts about Pi (π)
It's the most famous transcendental number ever, and March 14 (3/14 in many countries) is the perfect day to celebrate Pi Day!
The 14th of March is here, just like it is every year. There are many reasons to celebrate the day, but mathematicians in any country that writes the date as (month/day) should be especially happy to see the numbers "3" and "14" next to each other. This is because 3.14 is a good approximation for one of the most famous numbers that can't be written as a simple set of digits:. It's called "Pi Day" all over the world by people who like to bake, and it's a great time to share some facts about with the world.
Even a mathematician probably won't get to the end of this list and know all 11 of these facts about. The first two facts are well-known, but I doubt anyone, not even a mathematician, will know all 11. See how well you can do by following along.
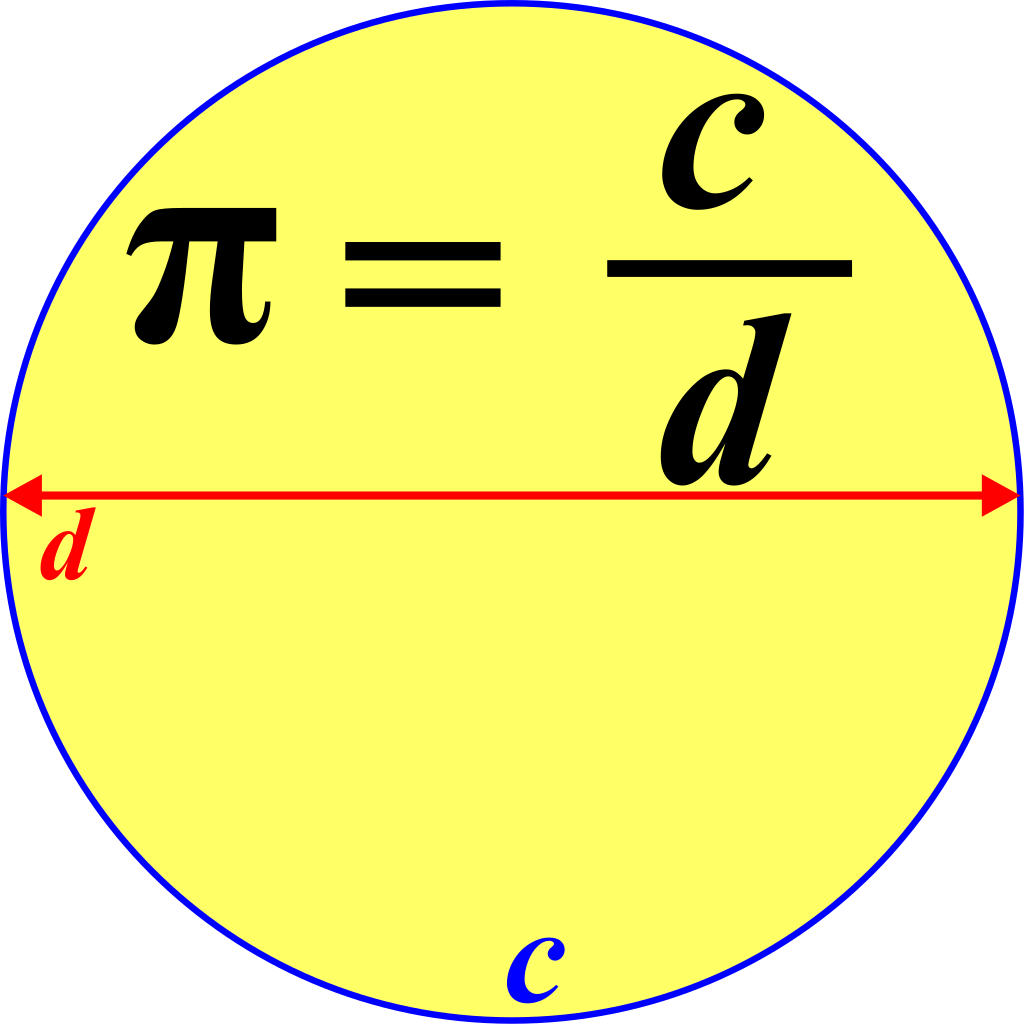
1.) Pi, or π as we’re going to call it from now on, is the ratio of a perfect circle’s circumference to its diameter. When I first started teaching, one of the first things I had my students do was bring in a "circle" from home. It could have been a pie tin, a paper plate, a mug with a circular bottom or top, or any other object with a circle on it. There was just one catch: I'd give you a flexible tape measure, and you'd have to measure both the circumference and the diameter of your circle.
Between all of my classes, there were more than 100 students. Each student measured the circumference of their circle and divided it by the diameter of their circle. This should have given an approximation for. As it turns out, every time I do this experiment and take the average of all the students' results, the average is always between 3.13 and 3.15, often right at 3.14, which is the best three-digit estimate of. Even though there are many better ways to get close to than the crude one I used, this is the best that you can do.
2.) π cannot be calculated exactly, because it is impossible to represent as a fraction of exact (integer) numbers. If you can write a number as a fraction (or ratio) between two integers, which are whole numbers that can be positive or negative, then you know exactly what that number is. This is true for numbers like 2/5 (or 0.4) whose fractions don't repeat and for numbers like 2/3 (or 0.666666...) whose fractions do repeat.
But, like all irrational numbers, can't be shown this way, and because of that, it can't be calculated exactly. We can only come close to, and we've been doing that quite well for a long time, even going back thousands of years.
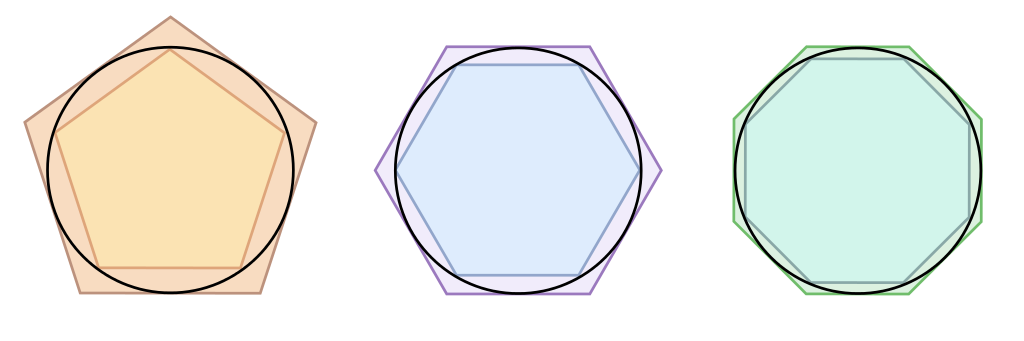
3.) The “method of Archimedes” has been used to approximate π for more than 2000 years.
It's hard to figure out the area of a circle if you don't already know what "" is. But it's easy to figure out the area of a regular polygon if you know the formula for a triangle's area and know that any regular polygon can be broken up into a series of isosceles triangles. You can go one of two ways:
- you can inscribe a regular polygon inside of a circle, and know that the “true” area of your circle must be bigger than that,
- or you can circumscribe a regular polygon about the outside of a circle, and know that the “true” area of your circle must be less than that.
The more sides you make to your regular polygon, in general, the closer you’ll get to the value of π. In the 3rd century BC, Archimedes took the equivalent of a 96-sided polygon to approximate π, and found that it must lie between the two fractions 220/70 (or 22/7, which is why π day in Europe is the 22nd of July) and 223/71. The decimal equivalents for those two approximations are 3.142857… and 3.140845…, which is pretty impressive for some 2000+ years ago!

4.) The approximation for π known as Milü, discovered by Chinese mathematician Zu Chongzhi, was the best fractional approximation of π for about 900 years: the longest “best approximation” in recorded history.
A mathematician named Zu Chongzhi found a remarkable fractional approximation of : 355/113 in the 5th century. If you like to estimate in decimal form, this comes out to 3.14159292035... which gets the first seven digits of right and is only off by about 0.0000002667, or 0.00000849% of the real value.
In fact, if you calculate the best fractional approximations of as a function of increasing denominator: starting with the fraction "3/1" and increasing either the numerator or denominator, you can get better and better fractional approximations of, with 355/113 being the best approximation with a diameter less than 10,000.
You won't find a better one until you find 52163/16604, which is just a little bit better. The difference between 355/113 and the real value of is 0.00000849%, but the difference between 52163/16604 and the real value of Pi is 0.00000847%.
This amazing fraction, 355/113, was the best way to get close to until the 14th or 15th century, when the Indian mathematician Madhava of Sangamagrama came up with a better way to get close to by adding up an infinite number of series.
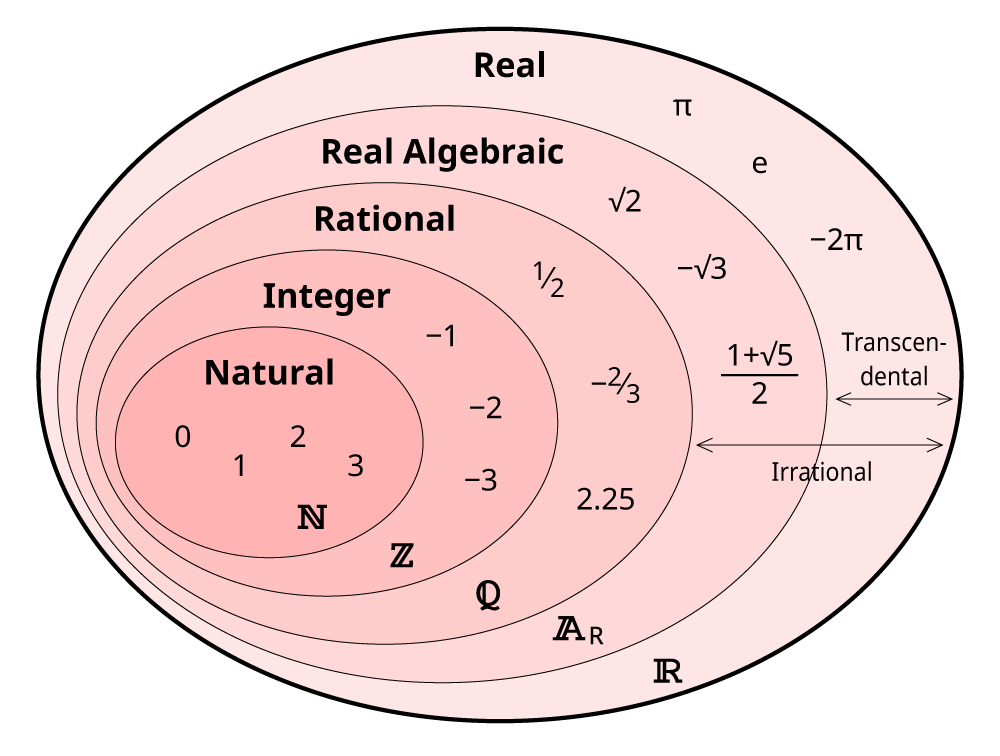
5.) π is not only an irrational number, but it’s also a transcendental number, which has a special meaning. In order to be a rational number, you need to be able to express your number as a fraction with integers for their numerator and a denominator. By that account, π is irrational, but so is a number like the square root of a positive integer, such as √3. However, there’s a big distinction between a number like √3, which is known as a “real algebraic” number, and π, which is not just irrational but also transcendental.
The difference?
If you can write down a polynomial equation with integer exponents and factors, and only use sums, differences, multiplication, division, and exponents, all of the real solutions to that equation are real algebraic numbers. For example, √3 is a solution to the polynomial equation, x² – 3 = 0, with -√3 as its other solution. But no such equations exist for any transcendental numbers, including π, e, and γ.
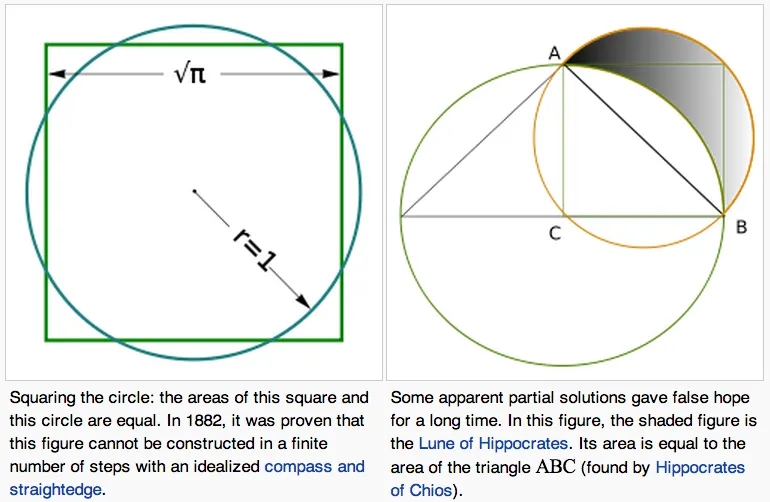
In fact, one of history’s most famous unsolved math puzzles is to create a square with the same area as a circle using only a compass and straightedge. In fact, the difference between the two types of irrational numbers, real algebraic and transcendental ones, can be used to prove that constructing a square whose length has a side of “√π” is impossible given a circle of area “π” and a compass and a straightedge alone.
Of course, this wasn’t proven until 1882, showing just how complicated it is to rigorously prove something that seems obvious (upon exhausting yourself) in mathematics!
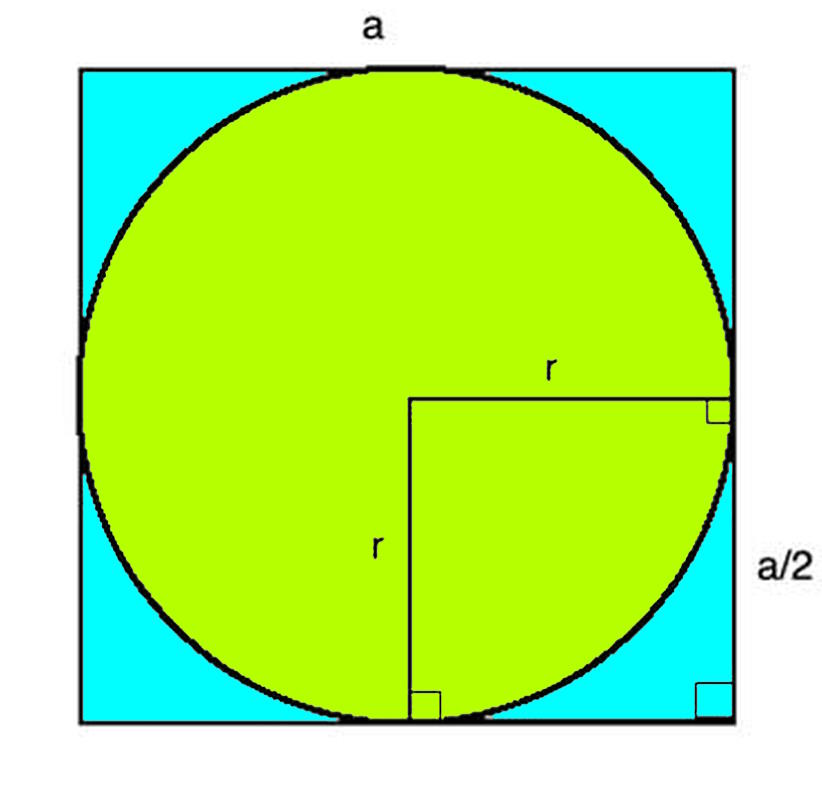
6.) You can very simply approximate π by throwing darts. Want to approximate π, but don’t want to do any mathematics more advanced than simply “counting” to get there?
No problem, simply take a perfect circle, draw a square around it, where one side of the square is exactly equal to the diameter of the circle, and start throwing darts. You’ll immediately find that:
- some of the darts land inside the circle (option 1),
- some of the darts land outside the circle but inside the square (option 2),
- and some darts land outside both the square and circle (option 3).
As long as your darts are truly landing in a random location, you’ll find that the ratio of “the darts that land inside the circle (option 1)” to “the darts that land inside of the square (options 1 and 2 combined)” is precisely π/4. This method of approximating π is an example of a simulation technique very commonly used in particle physics: the Monte Carlo method. In fact, if you write a computer program to simulate this type of dartboard, then congratulations, you’ve just written your first Monte Carlo simulation!
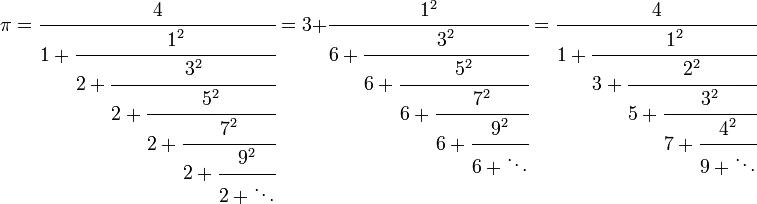
7.) You can very excellently, and relatively quickly, approximate π by using a continued fraction. Although you can’t represent π as a simple fraction, just as you can’t represent it as a finite or repeating decimal, you can represent it as something known as a continued fraction, or a fraction where you calculate an increasing number of terms in its denominator to arrive at an increasingly superior (and accurate) approximation.
There are many examples of formulae that one can calculate, repetitively, to arrive at a good approximation for π, but the advantage of the three shown above is that they’re simple, straightforward, and provide an excellent approximation with only a relatively small number of terms. For example, using only the first 10 terms of the final series shown gives the first 8 digits of π correctly, with only a small error in the 9th digit. More terms means a better approximation, so feel free to plug in as many numbers as you like and see how satisfying it can be!

8.) After 762 digits of π, you arrive at a string of six 9s in a row: known as the Feynman Point. Now, we head into territory that requires some pretty deep calculations. Some have wondered, “What sort of patterns are there to find embedded within the number π?” If you write out the first 1,000 digits, you can find some interesting patterns.
- The 33rd digit of π, a “0,” is how far you have to go to get all 10 of the digits, 0-through-9, to appear in your expression for π.
- There are a few instances of “triply repeating” numbers in-a-row in the first 1,000 digits, including “000” (two times), “111” (two times), “555” (two times), and “999” (two times).
- But those two instances of “999” repeating are next to each other; after the 762nd digit of π, you actually get six 9s in a row.
Why is this so noteworthy? Because physicist Richard Feynman noted that if he could memorize π to “the Feynman Point,” he could recite the first 762 digits of π and then say, “nine-nine-nine-nine-nine-nine and so on…” and that would be extremely satisfying. It turns out that, although all consecutive combinations of digits can be proven to appear somewhere in π, you won’t find a string of 7 identical digits in a row until you’ve written out nearly 2 million digits of π!

9.) You can outstandingly approximate π, accurate to 31 digits, by dividing two mundane-appearing irrational numbers. One of the most bizarre properties of π is that it shows up in some really unexpected places. Although the formula eiπ = -1 is arguably the most famous one, perhaps a better and even more bizarre fact is this: if you take the natural logarithm of a particular 18 digit integer, 262,537,412,640,768,744, and you then divide that number by the square root of the number 163, you get a number that’s identical to π for the first 31 digits.
Why is this so, and how did we get such a good approximation for π?
It turns out that in 1859, mathematician Charles Hermite discovered that the combination of three irrational (and two transcendental) numbers e, π, and √163 make what’s known as an “approximate integer” by combining them in the following fashion: eπ√163 is almost exactly an integer. The integer that it almost is? 262,537,412,640,768,744; in fact it “equals” 262,537,412,640,768,743.99999999999925…, so rearranging that formula is how you get this incredibly good approximation for π.

10.) Four famous physics/astronomy and space heroes from history have their birthday on π day. Look at the image above, and you’ll see a collage of four faces, showing people of various levels of fame in physics/astronomy/space circles. Who are they?
- First up is Albert Einstein, born on March 14, 1879. Known for his contributions to relativity, quantum mechanics, statistical mechanics, and energy-mass equivalence, Einstein is also the most famous person out there with a π-day birthday.
- Next is Frank Borman, born on March 14, 1928, who turns 95 years old on this day in 2023. He commanded Gemini 7 and was NASA liaison at the White House during the Apollo 11 moon landing, but he is best known for commanding the Apollo 8 mission, which was the first mission to bring astronauts to the Moon, to fly around the Moon, and to photograph the site of Earth “rising” over the Moon’s horizon.
- The third image is perhaps the least known today, but is of Giovanni Schiaparelli, born March 14, 1835. His work during the 19th century gave us the greatest maps, of their time, of the other rocky planets within our Solar System: Mercury, Venus, and most famously, Mars.
- And the final image is of Gene Cernan, born March 14, 1934, who is (at present) the final and most-recent human to set foot on the Moon, as he re-entered the Apollo 17 lunar module after crewmate Harrison Schmitt. Cernan died on January 16, 2017 at the age of 82.

11.) And there’s a famous star cluster that truly looks like a “π” in the sky! Look at the image above; can you see it? This “pi”cturesque view is of the open star cluster Messier 38, which you can find by locating the bright star Capella, the third-brightest star in the northern celestial hemisphere behind Arcturus and Rigel, and then moving about a third-of-the-way back toward Betelgeuse. Right in that location, before you reach the star Alnath, you’ll find the location of the star cluster Messier 38, where a red-green-blue color composite clearly reveals a familiar shape.
Unlike the newest, youngest star clusters out there, none of the remaining stars in Messier 38 will ever go supernova; the survivors are all too low in mass for that. The most massive stars within the cluster have already died, and now, some 220 million years after these stars have formed, it’s only the A-class, F-class, G-class (Sun-like) and cooler stars which remain. And remarkably, the brightest, bluest survivors make an approximate π-shape in the sky. Even though there are four other star clusters that are relatively nearby, none of them are related to Messier 38, which is 4,200 light-years away and contains hundreds, perhaps even thousands of stars. For a real-life look at π-in-the-sky, simply find this star cluster and the sights are yours to behold!
Happy π day to one and all, and may you celebrate it in a sweet and fitting fashion!
Source: BigThink











